Physics: Ray Optics and Optical Instruments

Reflection:-


Light:- it is an agent which produces in us the sensation of sight. It is a form of energy.


Transparent medium:- It is a medium through which light can be propagated easily.(e.g., sun, candle, electric arc)


Translucent medium:- It is a medium through which light is propagated partially.(e.g., paper, ground, glass)


Opaque:- It is a medium through which light can be propagated. (e.g., wood, iron)


Reflection:- It is the property of light by virtue of which, light is sent back into the same medium from which it is coming after being obstructed by a surface.


Laws of reflection:-



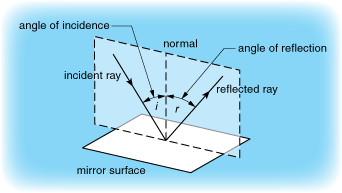?(a) The incident ray, the reflected ray and normal to the reflecting surface at the point of incidence, all lie in one plane and that plane is perpendicular to the reflecting surface.

(b) The angle of incidence is equal to the angle of reflection.

So, ∠i = ∠r


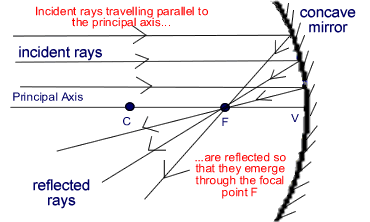
Concave mirror:- It is a spherical mirror which when looked from the reflecting side is depressed at the center and bulging at the edges.






Convex mirror:-





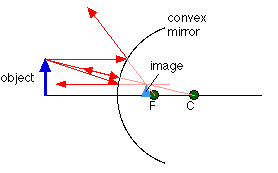
?It is a spherical mirror which when looked from the reflecting side bulges at the center and is depressed at the edges.


Radius of curvature(R):-



Radius curvature of a mirror is defined as the radius of that sphere of which the mirror forms a part.


Principal focus:-



Principal focus is a point, situated on the principal axis, at which a beam coming parallel to principal axis meets or appears to meet after reflection from the mirror.


Focal plane:-



It is a vertical plane passing through the principal focus and perpendicular to the principal axis.


Focal length (f):-



Focal length, of a spherical mirror is the distance of its principal focus from its pole.


Relation between focal length and radius of curvature:-



f = R/2

This signifies, the focal length of a spherical mirror is half of its radius of curvature.


Mirror formula:-



?1/f = 1/v + 1/u = 2/r


Relative positions, size and nature of image as object is brought from infinity to the pole of a concave mirror:-



(a) If the object is at infinity, u = ∞

v = -f , m = 0

Thus, image is obtained at the focus of a focal plane and very small in dimensions.

(b) If object lies beyond center of curvature,

2f > v >f

(c) If object is at center of curvature,

v = -2f , m =1

Thus, a real and inverted image of same size as that of object is formed at center of curvature.

(d) Object is in between a distance fand 2f , i.e., in between focus and center of curvature (f < u < 2f):-

v < ∞ and m = (v/u) >1

Thus, a real, inverted and magnified image is formed in between center of curvature and infinity.

(e) Object is kept at focus (u = -f):-

v = -∞

The rays after reflection are rendered into a parallel beam meeting in infinity.

(f) Object is kept within focus (u < -f):-

v is positive.

Thus, a virtual, erect and magnified image is formed on the other side of mirror.

Some important points:-


(a) In case of spherical mirrors, focal length is half its radius of curvature image.

(b) In case of concave mirror areal object produces a real and inverted if its distance from pole is greater than the focal length while its virtual and erect if its distance from pole is less than focal length.

(c) In case of convex mirror a real object always produces a virtual and erect image.

(d) All real images are inverted and virtual images are erect.

Refraction:-


Refraction:- Refraction is the phenomenon by virtue of which a ray of light going from one medium to the other undergoes a change in its velocity.




Incident ray:-The ray which approaches the interface is called incident ray.


Refracted ray:- Ray which goes into the second medium is called angle of incidence.


Laws of refraction:-



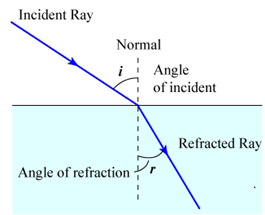?(a) Snell’s law:- The sine of the angle of incidence bears a constant ratio with the sine of the angle of refraction.

sin i/sin r = constant

(b) The incident ray, the refracted ray and the normal to the interface at the point of incidence all lie in one plane and that plane is perpendicular to the interface separating the two media.

Refractive Index:-


?(a) Refractive index of a medium with respect to another is defined as the ratio between sine of the angle of incidence to the sine of angle of refraction.

sin i/sin r = constant = 1µ2

(b) Refractive index of medium 2 with respect to1 is also defind as the ratio between velocity of light in medium 1 to the velocity of light in medium 2.

(c) 1µ2 = v1/v2

(d) µ = c/v

(e) Refractive index of a second medium with respect to first is defined as the ratio between absolute refractive index of second medium to the abdsolute refractive index of first medium.

(f) 1µ2 = µ2/µ1?

?Total internal reflection:-


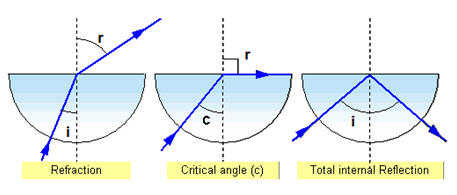?(a) Critical angle:- Critical angle is the angle of incidence of a ray of light in denser medium such that its angle of refraction in the rarer medium is 90º.

(b) Total internal reflection:- It is the phenomenon by virtue of which, a ray of light travelling from a denser to a rarer medium is sent back in the same medium provided, it is incident on the interface at an angle greater than critical angle.

(c) μ = 1/sin C

Refraction at a single spherical surface when light travelling from medium of refractive index μ1 (rarer) to that of refractive index μ2 (denser):-  


(a) Refraction at a convex surface producing real image:-

 μ2/v – μ1/u = μ2 - μ1/R

(b) Refraction at a convex surface producing virtual image:-

 μ2/v – μ1/u = μ2 - μ1/R

(c) Refraction at a concave surface:-

μ2/v – μ1/u = μ2 - μ1/R

Refraction at a single spherical surface when light travelling from medium of refractive index μ2 (denser) to that of refractive index μ1(rarer) :-


Convex surface producing a real image of a real object:-

μ2/u – μ1/v = μ2 - μ1/R

Light travelling from air to glass:-


μ/v – 1/u = μ-1/R

Light travelling from glass to air:-


μ/u – 1/v = μ-1/R

Principal focal length:-


(a) Second principal focal length:- Second principal focal length of a surface is the distance of that point from the pole of the surface at which a beam coming parallel to principal axis meets or appears to meet after refraction through the surface.

f2 = μ2R/ [μ2 - μ2]

(b) First principal length:- First principal focal length of a surface is defined as the distance of that point from the pole of surface from where if a beam diverges or to which a beam converges, the rays after refraction through the surface become parallel to principal axis.

f1 = -μ1R/ [μ2 – μ1]

(c) Relation between f1 and f2:-

f2/v + f1/u = 1

Lens:-


A portion of refracting material bound between two spherical surfaces is called a lens.

Converging lens:-


A lens is said to be converging if the width of the beam decreases after refraction through it.

Diverging lens:-


A lens is said to be diverge if the width of the beam increases after refraction through it.

Center of curvature:-


Center of curvature of a surface of a lens is defined as the center of that sphere of which that surface forms a part.

Radius of curvature:-


Radius of curvature of a surface of a lens is defined as the radius of that sphere of which the surface forms a part.

Lens formula:-


1/f = 1/v – 1/u

Linear magnification:-


It is the ratio between the size of the image to the size of the object.

m = I/O 

Expression for m in terms of u, v and f :-


(a) In terms of v and f:- m = [f-v] / f

(b) In terms of u and f:- m = f / [f+u]

Position of the image as the object is gradually moved from infinity to the pole of the lens:-


(a) Object being at infinity:- v = f, Magnification in this case is extremely small and the image is said to be real and inverted.

(b) Object lying beyond 2f:- 2f > v > -f, m(= v/u) always is less than one.

(c) Object at 2f:- v = 2f, m = -1

(d) Object lying between f and 2f:- v>2f, m(= v/u) always is greater than one.

(e) Object at f:- v = ∞, m(= v/u) is infinite.

(f) Object lying between f and optical center C:-

At f, u = -f. So, v = ∞

At C, u = 0, So, v = 0


Refraction through a thin double convex lens when the medium on the two sides of the lens is same (Lens maker’s formula):-



1/f = (μ – 1) (1/R1 – 1/R2)


Refraction through a thin double convex lens when the medium situated on the two sides of the lens is different:-



1/f = [[μ3 – μ1]/μ3R1] + [[μ3 – μ2]/μ3R2]

Double concave lens:-


(a) When the medium situated on the two sides of the lens is same:-

1/f = (μ – 1) (1/R1 – 1/R2)

(b) When the medium situated on the two sides of the lens is different:-

1/f = [[μ3 – μ1]/μ3R1] + [[μ3 – μ2]/μ3R2]

Combination of two convex lenses in contact:-


F = f1f2 / f1+ f2

Power of a lens:-


The reciprocal of the focal length of a lens, expressed in meter, is called its power.

P = 1/f

Refraction through a prism:-


μ = sin [(A+dm)/2] / sin [A/2]

Here, dm is the minimum angle of deviation.

Refraction through a prism for small angle of incidence:-


d = A (μ-1)

This signifies that the angle of deviation d is independent of the angle of incidence, provided it is small.

Dispersion:-


Dispersion:- The splitting of light into its constituent colors is called dispersion.


Cauchy’s formula:- μ = A+(B/λ2)+…



Here A and B are constants and λ is the wavelength of light.


Refraction through a prism:-



(a) Deviation:- A ray of monochromatic light (light possessing one wave-length only), while passing through a prism suffers a change in its path, the phenomenon is known as deviation.

d = (μ-1) A

Here A is the refractive angle of prism and μ is the refractive index of the material of prism for that particular wave length of light.

(b) Dispersion:- A ray of light (containing more than one wavelengths), while passing through the prism splits up into a number of rays. The phenomenon is called dispersion.

dv = (μv-1) A

dr = (μr-1) A

Here dv is deviation for violet and dr is the deviation for red color. μv and  μrbe the refractive indices of the material of prism for violet and red colors.

Since, μv > μr, therefore dv is greater than dr.

Dispersive power (ω):- Dispersive power of a prism is defined as the ratio between angular dispersion to mean deviation produced by the prism.


ω = (dv - dr)/d = (μv – μr)/(μ-1) = dμ/(μ-1)

Spectrum:- The band of colors lying side-by-side is called spectrum.


(a) Impure spectrum:- Impure spectrum is a spectrum in which the constituent colors overlap each other.

(b) Pure spectrum:- Pure spectrum is a spectrum in which all the constituent colors occupy different and distinct positions.

Optical Instruments:-

Power of a concave lens (P):-


         P = (100/x) dioptre, Here ‘x’ is the distance of far point of the defective eye, in ‘cm’.

Magnifying power or magnification of a simple microscope:-


?         M = 1+ (D/f),

         Here, ‘D’ is the distance of distinct vision and ‘f’ is the focal length.

Magnifying power or magnification of a compound microscope:-


?          M = L/f0[1+(D/fe)]

          f0 is the focal length of object, fe is the focal lengthy of eyepeice and L is the length of microscope tube.

Magnifying power or magnification of astronomical telescope (Normal Adjustment):-


           M = f0/fe

Magnifying power or magnification of astronomical telescope (When the final image is formed at the distance of distinct vision):-


          M = (f0/fe) [(fe+D)/D]

Magnifying power or magnification of Galileo’s telescope:-


          M = F/f