Sunday, May 27, 2018

Chemistry: Chemical Kinetics 


Rate of Reaction:


    

  • 
Rate of change of extent of reaction is the rate of reaction.
    

    • 

  • 
Rate of reaction is positive for product and negative for reactant.
    

    • 

  • 
For reaction aA →bB
Rate =1/b(Δ[B]/ Δ t)  = -1/a (Δ [A]/ Δt)
    

    • 

  • 
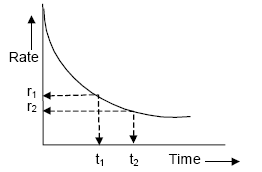
It goes on decreasing as the reaction progress due to decrease in the concentration(s) of the reactant(s).
    

    

    

    

    

    • 







    

  • 
Unit of rate of reaction : mol L-1 s-1
    

    • 

  • 
The rate measured over a long time interval is called average rate and the rate measured for an infinitesimally small time interval is called instantaneous rate.
    

    • 

  • 
In a chemical change, reactants and products are involved. As the chemical reaction proceeds, the concentration of the reactants decreases, i.e., products are produced.
    

    • 

  • 
The rate of reaction (average rate) is defined as the change of concentration of any one of its reactants (or products) per unit time.
    

    • 




Order of Reaction







 







For reaction aA + bB + ….. → cC+ ….



R ∝[A]m[B]n or R = k[A]m[B]n….



Where m and n may or may not be equal to a & b.



m is order of reaction with respect to A and n is the order of reaction with respect to B.



m + n +… is the overall order of the reaction.



Elementary Reaction:


    

  • 
It is the reaction which completes in a single step.
    

    • 

  • 
A reaction may involve more than one elementary reactions or steps also.
    

    • 

  • 
Overall rate of reaction depends on the slowest elementary step and thus it is known as rate determining step.
    

    • 




Molecularity of Reaction:


    

  • 
Number of molecules taking part in an elementary step is known as its molecularity.
    

    • 

  • 
Order of an elementary reaction is always equal to its molecularity.
    

    • 

  • 
Elementary reactions with molecularity greater than three are not known because collisions in which more than three particles come together simultaneously are rare.
    

    • 








Chemical Reaction



Molecularity





PCl5  →  PCl3 + Cl2   



Unimolecular





2HI  →  H2 + I2 



Bimolecular





2SO2 + O2  →  2SO3



Trimolecular





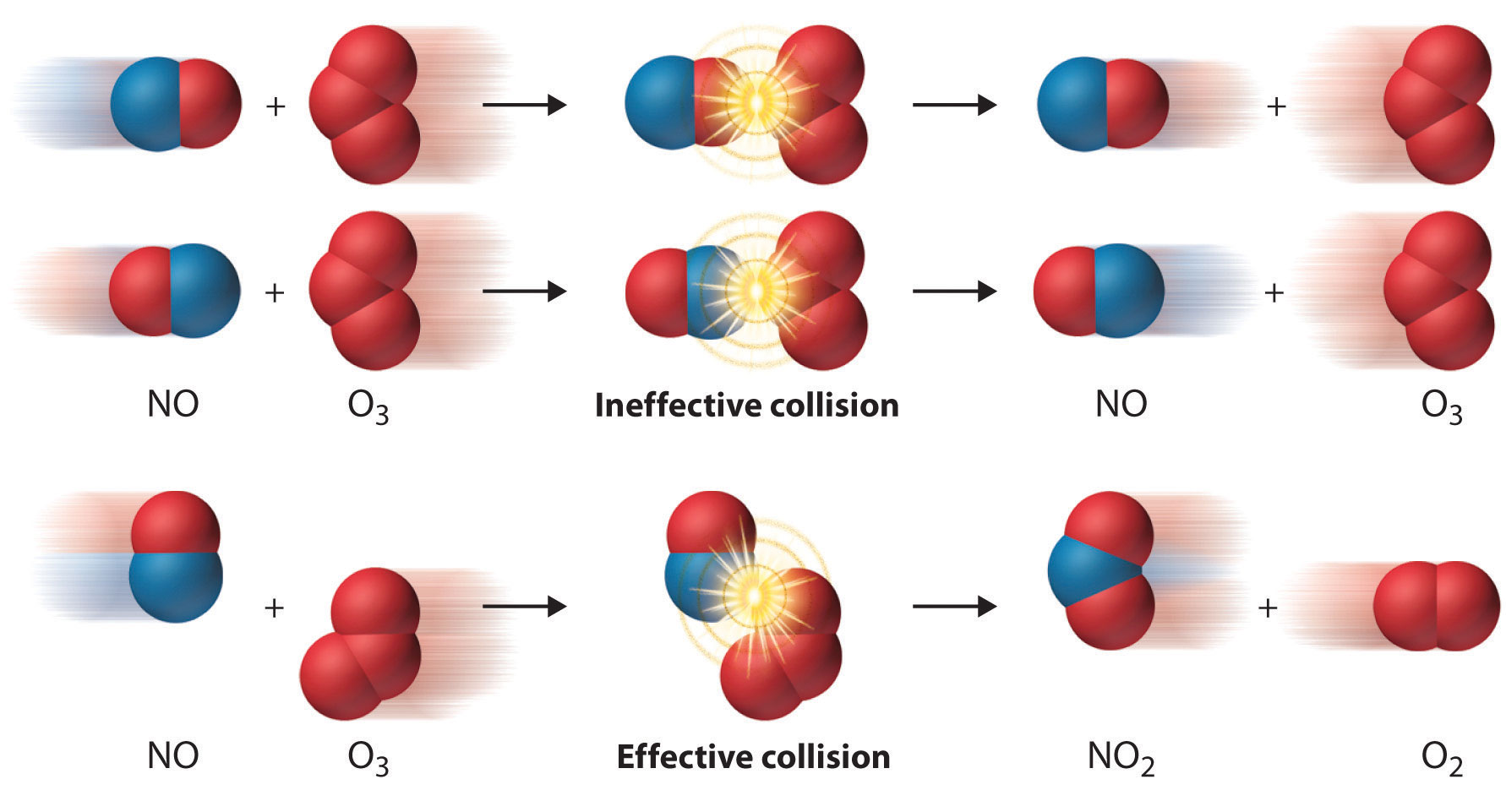
NO + O3  →  NO2 + O2



Bimolecular





2CO + O2  →  2CO2



Trimolecular





2FeCl3 + SnCl2 → SnCl2 + 2FeCl2



Trimolecular



 









Differential and Integrated Rate Laws:



Zero Order Reactions:



Characteristic of Zero Order Reaction



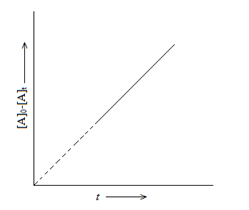
For Reaction: A → Product



[A]0-[A]t  = k0t



Where,



[A]0 = Initial concentration of A



[A]t = Concentration of A at time t.  



k0  =  Rate constant for zero order reaction.



Half Life:



t1/2 = [A]0/2k



Unit of rate constant = mol dm-3s-1



Examples: 


    

  • 
 Enzyme catalyzed reactions are zero order with respect to substrate concentration.
    

    • 

  • 
 Decomposition of gases on the surface of metallic catalysts like decomposition of HI on gold surface.
    

    • 




First Order Reactions:



Characteristic of First Order Reaction



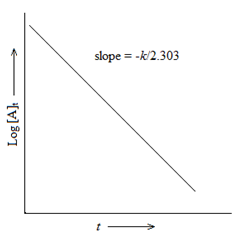
A → Product



(Δ [A] /A) = -k1Δt



 or k1=( 2.303/ t)log ([A]0 / [A]t) 



Half Life:



t1/2 = 0.693/k1



Half life is independent of the initial concentration of the reactant for a first order reaction.



Units of k1 =  s-1



Examples:



N2O5 →  2NO2 + 1/2O2



Br2 → 2Br



2HNO3 → 2NO + H2O



 H2O2→ H2O + 1/2O2 



Pseudo First Order Reactions:



These are the reactions in which more than one species is involved in the rate determining step but still the order of reaction is one.



Examples:


    

  • 
Acid hydrolysis of ester: CH3COOEt + H3O+ →CH3COOH + EtOH 
    

    • 

  • 
Inversion of cane sugar:
    

    • 




  


    

  • 
Decomposition of benzenediazonium halides C6H5N=NCl +H2O → C6H5OH +N2+HCl
    

    • 




Half – Life of a nth Order Reaction:



kt1/2 =  (2n-1-1)/(n-1)[A0]n-1



Where, n = order of reaction ≠1



Parallel  Reactions:



The reactions in which a substance reacts or decomposes in more than one way are called parallel or side reactions.





reaction-in-which-a-decomposes





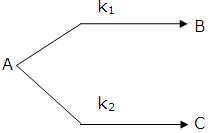
If we assume that both  of them are first order, we get.



-\frac{d[A]}{dt} = (k_1 +k_2) [A] =k_{av}[A]



k1 = fractional yield of B × kav



k2 = fractional yield of C × kav



If k1 >  k2 then



A → B main and



A → C is side reaction



Let after a definite interval x mol/litre of B and y mol/litre of C are formed.



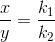
\frac{x}{y} =\frac{k_1}{k_2}



i.e



\frac{\frac{d[B]}{dt}}{\frac{d[C]}{dt}} =\frac{k_1}{k_2}



This means that irrespective of how much time is elapsed, the ratio of concentration of B to that  of C from the start (assuming no B  and C in the beginning ) is a constant equal to k1/k2.











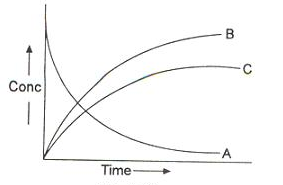
Sequential Reactions:



This reaction is defined as that reaction which proceeds from reactants to final products through one or more intermediate stages. The overall reaction is a result of several successive or consecutive steps.



A → B → C and so on



A\overset{k_1}{\rightarrow}B\overset{K_2}{\rightarrow}C



-\frac{d[A]}{dt} = k_1[A]…....(i)



\frac{d[B]}{dt} = k_1[A]-K_2[B]…......(ii)



\frac{d[C]}{dt} = k_2[B]….......(iii)



Integrating equation (i), we get



[A]-[A]_oe^{-k_1t}







   



   



 







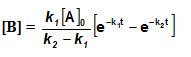
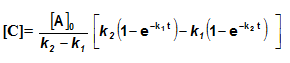
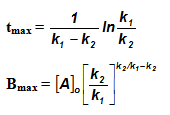
Arrhenius Equation:



k = A exp(-Ea/RT)



Where, k = Rate constant



A = pre-exponential factor



Ea = Activation energy



     ln k vs 1/T plot for Arrhenius Equation 



Temperature Coefficient: 



The temperature coefficient of a chemical reaction is defined as the ratio of the specific reaction rates of a reaction at two temperature differing by 10oC.



μ = Temperature coefficient= k(r+10)/kt



Let temperature coefficient of a reaction be ' μ ' when temperature is raised from T1to T2; then the ratio of rate constants or rate may be calculated as



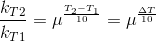
\frac{k_T_2}{k_T_1}=\mu ^\frac{{T_2-T_1}}{10} =\mu ^{\frac{\Delta T}{10}}



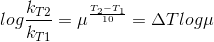
log\frac{k_T_2}{k_T_1}=\mu ^\frac{{T_2-T_1}}{10} =\Delta T log\mu



\frac{k_T_2}{k_T_1}= antilog[\frac{\Delta T}{10 }] log\mu



Its value lies generally between 2 and 3.



Collision Theory of Reaction Rate


    

  • 
A chemical reaction takes place due to collision among reactant molecules.
    

    • 

  • 
The number of collisions taking place per second per unit volume of the reaction mixture is known as collision frequency (Z).
    

    • 

  • 
The value of collision frequency is very high, of the order of 1025 to 1028 in case of binary collisions.
    

    • 

  • 
Every collision does not bring a chemical change.
    

    • 

  • 
The collisions that actually produce the products are effective collisions.
    

    • 

  • 
The effective collisions which bring chemical change are few in comparison to the form a product are ineffective elastic collisions, i.e., molecules just collide and
    

    • 

  • 
disperse in different directions with different velocities.
    

    • 

  • 
For a collision to be effective, the following two barriers are to be cleared.
    

    • 



    

  1. 
Energy Barrier
    

    2. 

  2. 
Orientation Barrier
    

    3. 








Radioactivity:



All radioactive decay follow 1st order kinetics



For radioactive decay A ->B



-(dNA/dt) =l NA



Where, l =  decay constant of reaction



NA  = number of nuclei of the radioactive substance at the time when rate is calculated.



Arrhenius equation is not valid for radioactive decay.



Integrated Rate Law: Nt = Noe-lt



Half Life:  t1/2= 0.693/λ



Average life time: Life time of a single isolated nucleus, tav= 1/λ



Activity: Rate of decay



A = dNA/dt, Also, At = Aoe-lt



Specific Activity: activity per unit mass of the sample.







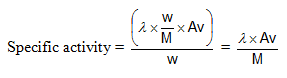
Units: dps or Becquerrel

0 comments:

Post a Comment

Subscribe to: Post Comments (Atom)