Physics: Gravitation

Gravitation:-


Kepler’s first law (law of elliptical orbit):-A planet moves round the sun in an elliptical orbit with sun situated at one of its foci.


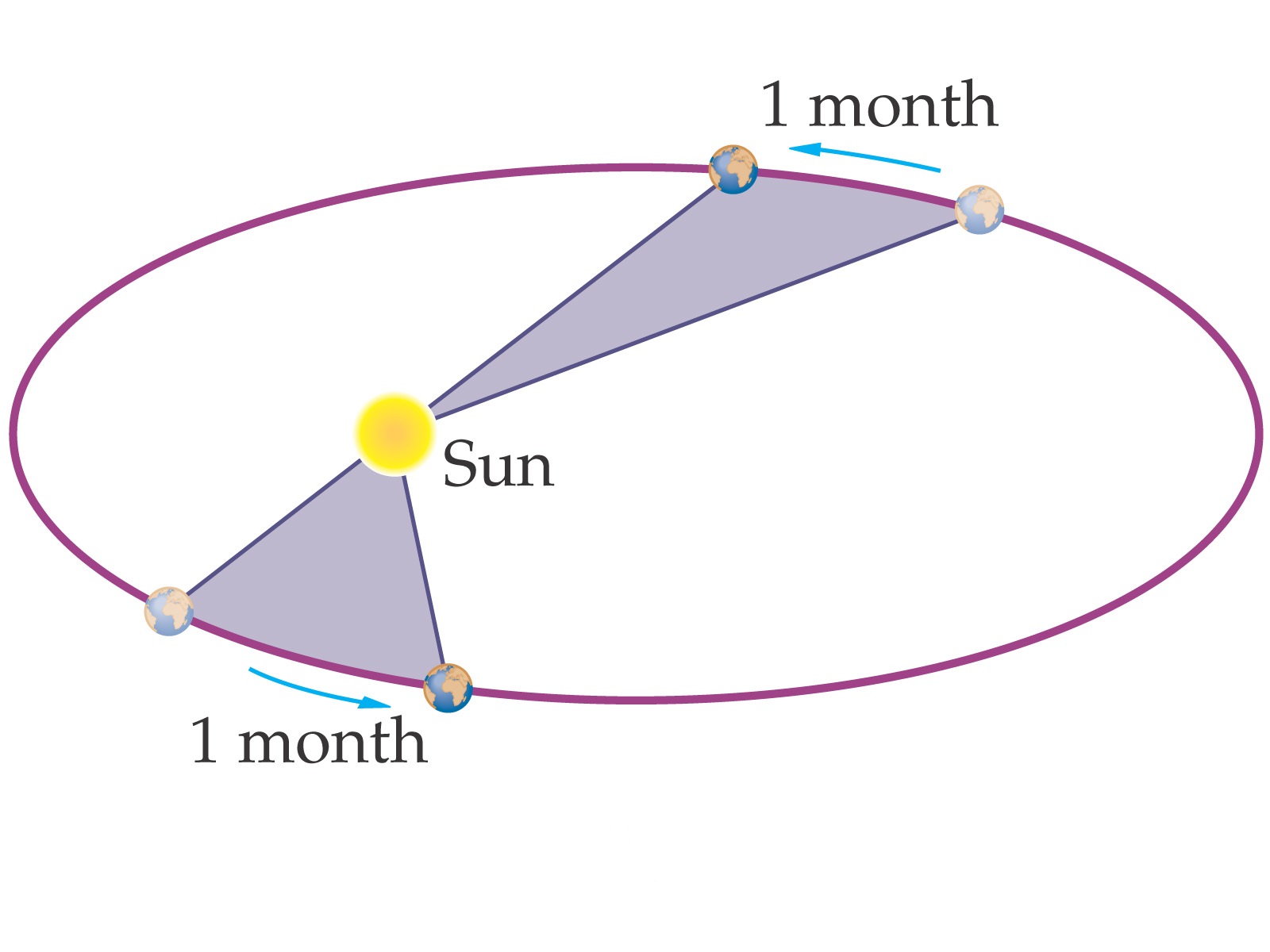
Kepler’s second law (law of areal velocities):- A planet moves round the sun in such a way that its areal velocity is constant.


Kepler’s third law (law of time period):-A planet moves round the sun in such a way that the square of its period is proportional to the cube of semi major axis of its elliptical orbit.



T2 ∝ R3

Here R is the radius of orbit.

T2 = (4π2/GM)R 3


Newton’s law of gravitation:-



Every particle of matter in this universe attracts every other particle with a forcer which varies directly as the product of masses of two particles and inversely as the square of the distance between them.

F= GMm/r2

Here, G is universal gravitational constant. G = 6.67 ´10 -11 Nm2 / kg2


Dimensional formula of G: G = Fr2/Mm =[MLT-2][L2]/[M2] = [M-1L3T-2]




Acceleration due to gravity (g):- g = GM/R2




Variation of g with altitude:- g' = g(1- 2h/R),  if h<<R. Here R is the radius of earth and h is the height of the body above the surface of earth.




Variation of g with depth:- g' = g(1- d/R). Here g' be the value of acceleration due to gravity at the depth d.




Variation with latitude:-



At poles:- θ = 90°, g' = g

At equator:- θ = 0°, g' = g (1-ω2R/g)

Here ω is the angular velocity.


As g = GMe/Re2 , therefore gpole > gequator


Gravitational Mass:- m = FR2/GM


Gravitational field intensity:-



E = F/m

= GM/r2


Weight:- W= mg


Gravitational intensity on the surface of earth (Es):-



Es = 4/3 (πRρG)

Here R is the radius of earth, ρ is the density of earth and G is the gravitational constant.


Gravitational potential energy (U):- U = -GMm/r



(a) Two particles: U = -Gm1m2/r

(b) hree particles: U = -Gm1m2/r12 –Gm1m3/r13 – Gm2m3/r23


Gravitational potential (V):- V(r) =  -GM/r



At surface of earth,

Vs=  -GM/R

Here R is the radius of earth.


Escape velocity (ve):-



It is defined as the least velocity with which a body must be projected vertically upward   in order that it may just escape the gravitational pull of earth.

ve = √2GM/R

or, ve = √2gR = √gD

Here R is the radius of earth and D is the diameter of the earth.


Escape velocity (ve) in terms of earth’s density:- ve = R√8πGρ/3




Orbital velocity (v0):-



v0 = √GM/r

If a satellite  of mass m revolves in a circular orbit around the earth of radius R and h be the height of the satellite above the surface of the earth, then,

r = R+h

So, v0 = √MG/R+h = R√g/R+h

In the case of satellite, orbiting very close to the surface of earth, then orbital velocity will be,

v0 = √gR


Relation between escape velocity ve and orbital velocity v0 :- v0= ve/√2  (if h<<R)




Time period of Satellite:- Time period of a satellite is the time taken by the satellite to complete one revolution around the earth.



T = 2π√(R+h)3/GM = (2π/R)√(R+h)3/g

If h<<R, T = 2π√R/g


Height of satellite:- h = [gR2T2/4π2]1/3 – R




Energy of satellite:-



Kinetic energy, K = ½ mv02 = ½ (GMm/r)

Potential energy, U = - GMm/r

Total energy, E = K+U

= ½ (GMm/r) + (- GMm/r)

= -½ (GMm/r)


Gravitational force in terms of potential energy:- F = – (dU/dR)




Acceleration on moon:-



gm = GMm/Rm2 = 1/6 gearth 

Here Mm is the mass of moon and Rmis the radius of moon.


Gravitational field:-



(a)    Inside:-

 

(b)   Outside:-

 


GRAVITATIONAL POTENTIAL & FIELD DUE TO VARIOUS OBJECTS





Causing Shape

Gravitational Potential (V)

Gravitational Field (I or E)

Graph

V vs R


POINT MASS


























AT A POINT ON THE AXIS OF RING











 






  












ROD


1. AT AN AXIAL POINT














 







V = –












2. AT AN EQUATORIAL POINT











































 


CIRCULAR ARC











 






































HOLLOW SPHERE






































SOLID SPHERE
















































LONG THREAD













V = ∞