Physics: Alternating Current

Alternating Current:-



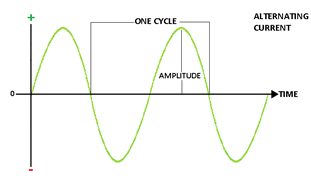An alternating current (a.c.) is a current which continuously, changes in magnitude and periodically reverses in direction.`

i = I0 sin ωt = I0 sin (2π/T) t

Here I0 is the peak value of a.c.

(a) Current, I =I0 sin ωt

(b) Angular frequency, ω= 2πn   (n is the frequency of a.c.)

(c) I =I0 sin 2πnt


Mean value of A.C or D.C. value of A.C.:-



Mean value of a.c. is that value of steady current which sends the same amount of charge, through a circuit, in same time as is done by a.c. in one half-cycle.

(Iav)half cycle = (2/π)I0

Thus, mean value of alternating current is 2/π times (0.637 times) its peak value.

(Vav)half cycle = (2/π) V0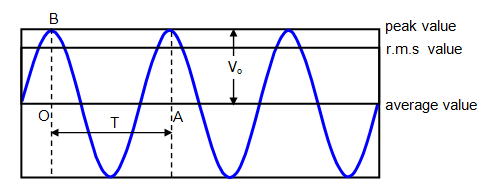


Average value of A.C. over a complete cycle:-



Iav = 0

The average value of a.c. taken over the complete cycle of a.c.is zero.


Root mean square value of a.c. or virtual value of a.c.:-



Root mean square value of alternating current is defined as that value of steady current which produces same heating effect, in a resistance, in a certain time as is produced by the alternating current in same resistance in same time. The r.m.s value of a.c.is also called its virtual value.

Irms = I0/√2

Root mean square value of alternating current is I/√2 times (or 0.707 times) the peak value of current.

Similarly, Vrms= V0/√2

Here V0 is the peak value of e.m.f.


Form Factor:-



Form Factor = rms value/average value = (V0/√2)/ (2 V0/π)  = π/2√2


Current elements:-



(a) Inductive reactance:- XL = ωL

Here, ω = 2πn, n being frequency of a.c.

L is the coefficient of self-inductance of coil.

(b) Capacitative reactance:- Xc = 1/ωC

Here C is the capacity of the condenser


Capacitor in AC circuit:-



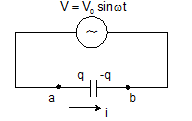q = CV0sinωt

I = I0 sin(ωt +π/2)

V0 = I0/ωC

Xc = 1/ωC


Inductor in AC circuit:-



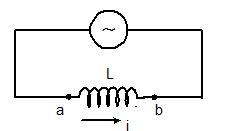VL = L(dI/dt) = LI0ω cosωt

I = (V0/ ωL) sinωt

Here, I0 = V0/ ωL

XL = ωL

And the maximum current, I0 = V0/XL


R-L circuit:-



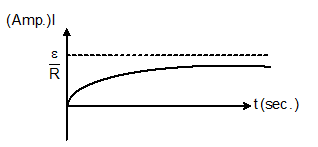
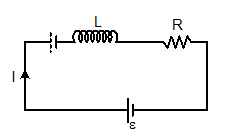I = ε/R [1-e-Rt/L]

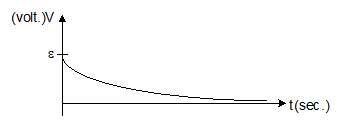
V = ε e-Rt/L


Graph between I (amp) and t (sec):-






Graph between potential difference across inductor and time:-






L-C Circuit:-



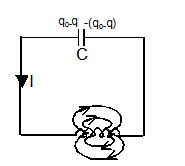f = 1/2π√LC

q = q0 sin (ωt+ϕ)

I = q0ωsin (ωt+ϕ)

ω = 1/√LC


The total energy of the system remains conserved,

½ CV2 + ½ Li2 = constant = ½ CV02 = ½ Li02




Series in C-R circuit:-





 V = IZ

The modulus of impedance, |Z |= √R2+(1/ωC)2

The potential difference lags the current by an angle, ϕ = tan-1(1/ωCR)


Series in L-C-R Circuit:





V = IZ

The modulus of impedance, |Z |= √[R2+(ωL-1/ωC)2]

The potential difference lags the current by an angle, ϕ = tan-1[ωL -1/ωC)/R]


Circuit elements with A.C:-





Circuit elements

Amplitude relation

Circuit quantity

Phase of V


Resistor

V0 = i0R

R

In phase with i


Capacitor

V0 = i0XC

C

Lags i by 90°


Inductor

V0 = i0XL

XL = wL

Leads i by 90°





Resonance:-



(a) Resonance frequency:- fr = 1/2π√LC

(b) At resonance, XL = XC, ϕ = 0, Z = R(minimum), cosϕ = 1, sinϕ = 0 nad current is maximum (=E0/R)


Half power frequencies:-



(a) Lower,  f1 = fr – R/4πL    or      ω1 = ωr – R/2L

(b) Upper,  f2 = fr + R/4πL    or      ω2 = ωr + R/2L


Band width:- Δf = R/2πL   or   Δf = R/L


Quality Factor:-



(a) Q = ωr/Δω = ωrL/R

(b) As ω = 1/√LC, So Q ∝ √L, Q ∝1/R and Q ∝ 1/√C

(c) Q = 1/ωrCR

(d) Q = XL/R   or  Q = XC/R 

(e) Q = fr/Δf   


At resonance, peak voltages are:-



(a) (VL)res = e0Q

(b) (VC)res = e0Q

(c) (VR)res = e0


Conductance, susceptance and admittance:-



(a) Conductance, G = 1/R

(b) Susceptance, S = 1/X

(c) SL = 1/XL and SC = 1/XC = ωC

(d) Admittance, Y = 1/Z

(e) Impedance add in series while add in parallel


Power in AC circuits:-



Circuit containing pure resistance:- Pav = (E0/√2)×(I0/√2) = Ev×Iv

Here Ev and Iv are the virtual values of e.m.f and the current respectively.

Circuit containing impedance (a combination of R,L and C):-

Pav = (E0/√2)×(I0/√2) cosϕ = (Ev×Iv) cosϕ

Here cosϕ is the power factor.

(a) Circuit containing pure resistance, Pav = EvIv

(b) Circuit containing pure inductance, Pav = 0

(c) Circuit containing pure capacitance, Pav = 0

(d) Circuit containing resistance and inductance,

Z = √R2+(ωL)

cosϕ = R/Z = R/[√{R2+(ωL)2}]

(e) Circuit containing resistance and capacitance:-

Z = √R2+(1/ωC)2

cosϕ = R/Z = R/[√{R2+(1/ωC)2}]

(f) Power factor, cosϕ = Real power/Virtual power = Pav/ErmsIrms


Transformer:-



(a) Cp = Np (dϕ/dt) and es = Ns (dϕ/dt)

(b) ep/es = Np/Ns

(c) As, epIp = esIs, Thus, Is/Ip = ep/es = Np/Ns

(d) Step down:- es < ep, Ns< Np and Is> Ip

(e) Step up:- es >ep, Ns>Np and Is< Ip

(f) Efficiency, η = es Is/ ep Ip


AC Generator:-



e = e0 sin (2πft)

Here, e0 = NBAω