Chemistry: Solutions

A solution is a homogeneous mixture of two (or more) substances, the composition of which may vary between certain limits. A solution consisting of two  components is called binary solution. The component which is present in large quantity is called solvent and the component which is small in quantity is called solute. If both components are in same physical state.

Type of Solutions

All the three states of matter (gas, liquid or solid) may behave either as solvent or solute. Depending on the state of solute or solvent, mainly there may be the following seven types of binary solutions.



S.No.

Solute

Solvent

Example


1

Gas

Gas

Air


2

Gas

Liquid

Aerated water (CO2 + H2O)


3

Gas

Solid

Hydrogen in palladium


4

Liquid

Liquid

Alcohol in water, benzene in toluene


5

Liquid

Solid

Mercury in zinc amalgam


6

Liquid

Gas

CO2 dissolved in water


 7

Solid

Liquid

Sugar in water, common salt in water


8

Solid

Gas

Smoke


9

Solid

Solid

Various alloys

 




Vapour Pressure: 


The pressure exerted by vapours over the liquid surface at equilibrium is called vapour pressure of the liquid.


If solute is non volatile solid or liquid the vapour pressure of solution is equal to partial vapour pressure of solvent in the solution.


If the solute is volatile solid or liquid, then vapour pressure will be equal to the sum of partial vapour pressure of solute and that of solvent.



Raoult’s Law:

“The partial vapour pressure of any component in the solution is directly proportional to its mole fraction”.




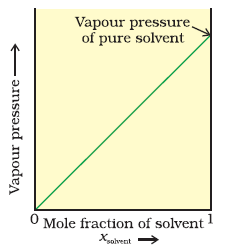
For a binary solution of two components A and B,

PA  = XA

PB = XB

Where

P0A  = vapour pressure of component A in pure state.

PA  = vapour pressure of component A in the solution.

P0B  = vapour pressure of component B in pure state.

PB  = vapour pressure of component B in the solution

Limitations of Raoult’s Law


Raoult’s law is applicable only to very dilute solutions.


It is applicable to solutions containing non-volatile solute only.


It is not applicable to solutes which dissociate or associate in a particular solution



Raoult’s Law in Combination with Dalton’s Law of Partial Pressure:

PT = XA P0A + XB P0B = P0B  + (P0A -P0B) XA                   

Where

PT = Total Vapour Pressure of the Solution.

Ideal and Non-Ideal Solutions:


Ideal Solution:



?These solutions obey Raoult’s law at all compositions of solute in solvent at all temperature 

Two liquids A and B form and ideal solution when A –A  and B–B molecular attractions will be same and hence A–B molecular attraction will be almost same as A–A and B–B molecular attraction.

For Ideal Solution:

1. dHmixing = 0, i.e. no heat should be absorbed or evolved during mixing

2. dVmixing  = 0, i.e. no expansion or contraction on mixing

Examples , Ethyl chloride and ethyl bromide, n–hexane and n–heptane , CCl4and SiCl4


Non-Ideal Solution:



?These solutions deviate from ideal behaviour and do not obey Raoult’s law over entire range of composition.  

For non ideal solutions,

1. dHmixing  ≠ 0

2. dHmixing ≠ 0

Here we may have two cases

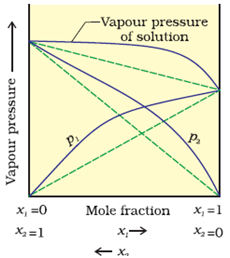
A) Positive Deviation:

1. PA  > XA & PB > XB

2. dHmix > 0

3. dVmix  > 0

Example: Cyclohexane and Ethanol



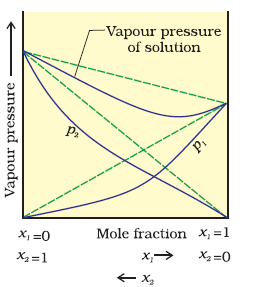
B) Negative Deviation:

1. PA  > XA & PB > XB

2. dHmix < 0

3. dVmix  < 0



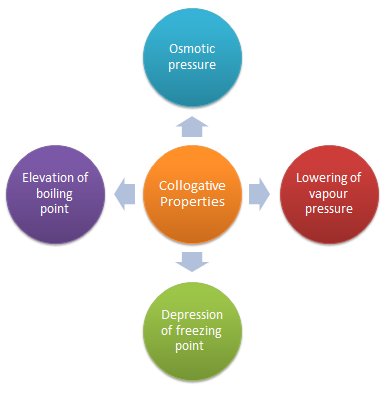
Colligative Properties

The properties of dilute solutions which depend only on number particles of solute present in the solution and not on their identity are called colligative properties (denoting depending upon collection).



Lowering of Vapour Pressure by a Non-Volatile Solute

The relative lowering of vapour pressure of a solution containing a non-volatile solute is equal to the mole fraction of the solute present in the solution.



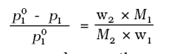
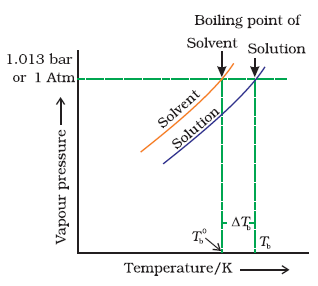
Elevation of Boiling Point by a Non-Volatile Solute :

Since the addition of a non-volatile solute lowers the vapour pressure of the solvent, the vapour pressure of a solution is always lower than that of the pure solvent, and hence it must be heated to a higher temperature to make its vapour pressure equal to atmospheric pressure.




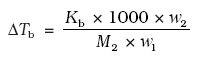
where M1 = molecular weight of solute and w2 and w1 are weights of solute and solvent

Depression of Freezing Point by a Non-Volatile Solute:




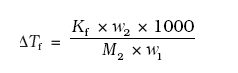
where M1 = molecular weight of solute and w2 and w1 are weights of solute and solvent

Osmosis and Osmotic Pressure:


Osmosis: The phenomenon of the passage of pure solvent from a region of lower concentration (of the solution) to a region of its higher concentration through a semi-permeable membrane.


Osmotic Pressure: Excess pressure which must be applied to a solution in order to prevent flow of solvent into the solution through the semi-permeable membrane.



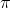V = nRT

where  

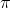   =    Osmotic pressure

V   =    volume of solution

n    =    no. of moles of solute that is dissolved

R   =    Gas constant

T    =    Absolute temperature

Isotonic Solutions: A pair of solutions having same osomotic pressure is called isotonic solutions.

Abnormal Molecular Weight and Van't Hoff  Factor:

Van't Hoff Factor:

Van't Hoff, in order to account for all abnormal cases introduced a factor i known as the Van't Hoff factor, such that



Degree of Association:

The fraction of the total number of molecules which combine to form bigger molecule



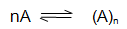
Let a be the degree of association, then,

The number of unassociated moles = 1-

The number of associated moles =/n

Total number of effective moles = 1-+/n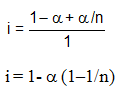 



Obviously,  i < 1

Degree of Dissociation  

The fraction of the total number of molecules which dissociates in the solution, that is, breaks into simpler molecules or ions.

KCl ↔  K+ + Cl-

1-           

Thus, the total number of moles after dissociation  = 1-++= 1+

Hence, i = (1+)/1

i = 1+ = 1+ (2–1)

In general, i = 1+ (n–1),

Where, n = number of particles ( ions) formed  after dissociation

From the above formula, it is clear that  i > 1